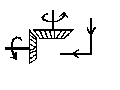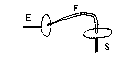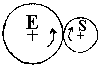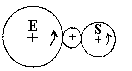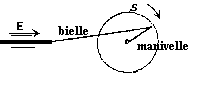MECANISMES

MECANISMES

A. LES MOUVEMENTS SIMPLES

1. LA TRANSLATION

On le dit de toute pièce ou ensemble mécanique se déplaçant en ligne droite. Tout point de la pièce décrit une ligne droite ou trajectoire rectiligne (ex : le tiroir, l'ascenseur, l'aiguille de la machine à coudre...)

2. LA ROTATION

On le dit de toute pièce ou ensemble mécanique tournant autour d'un axe central. Tout point de la pièce décrit un cercle. (ex : les ailes du moulin, une roue de bicyclette, les aiguilles d'une montre...)

A noter : certaines pièces n'effectuent pas un tour complet, on a une rotation partielle. (ex : le balancier d'une horloge, la poignée d'une porte)

B. LES GUIDAGES

1. LE GUIDAGE EN TRANSLATION

Il est en général assuré par un système de glissières.

2. LE GUIDAGE EN ROTATION

1er cas : La roue tourne autour d'un axe fixe, le guidage est assuré par le moyeu de la roue. Il faut prévoir un blocage en translation.

2ème cas : La roue est fixe sur l'arbre, le guidage est assuré par des supports ou paliers de l'arbre.

C. LA TRANSMISSION DU MOUVEMENT DE ROTATION

Problème posé : La roue menante ou roue motrice E (entrée du système) tourne. Comment transmettre le mouvement de rotation à la roue menée S (sortie du système) ?

NE est la fréquence de rotation à l'entrée du système (en tours/mn)
NS est la fréquence de rotation à la sortie du système (en tours/mn)

La raison R est définie par R = NS / NE

si R > 1     il y a multiplication de la vitesse (la transmission est dite surmultipliée)

si R = 1     la transmission est simple

si R < 1     il y a réduction de la vitesse (la transmission est dite démultipliée)

Il existe plusieurs solutions :

1. LA TRANSMISSION DIRECTE PAR FRICTION .

Les roues E et S sont en contact

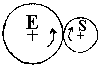
Si DE est le diamètre de la roue E et DS celui de la roue S, on a :
NE x DE = NS x DS et R = NS / NE = DE / DS (si le système ne patine pas).

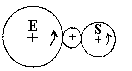
La roue intermédiaire ne change pas NS mais change son sens de rotation.

2. LA TRANSMISSION DIRECTE PAR ROUES DENTEES

On a un engrenage simple (ensemble de 2 roues dentées)

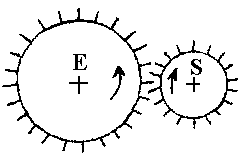Si ZE est le nombre de dents de la roue E et ZS celui de la roue S, on a :
NE x ZE = NS x ZS et R = NS / NE = ZE / ZS.
Une roue dentée intermédiaire ne change pas NS mais change son sens de rotation. Un train d'engrenages est constitué par un ensemble de roues dentées.

Le changement de direction d'un mouvement est assuré par des pignons coniques.

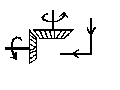3. LA TRANSMISSION INDIRECTE PAR COURROIE

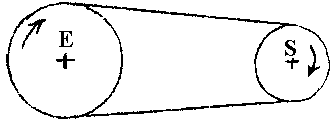
On a NE x DE = NS x DS et R = NS / NE = DE / DS

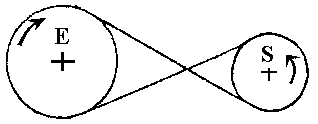
Le croisement de la courroie permet l'inversion du sens de rotation.

4. LA TRANSMISSION INDIRECTE PAR ROUES DENTEES ET CHAINE

On a NE x ZE = NS x ZS et R = NS / NE = ZE / ZS

5. LA TRANSMISSION PAR CARDAN

On a R = 1

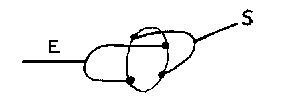6. LA TRANSMISSION PAR ROUE DENTEE ET VIS SANS FIN

On a R = 1 / ZS

7. LA TRANSMISSION PAR FLEXIBLE

On a R = 1

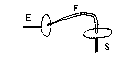D. COMMENT MODIFIER LES MOUVEMENTS

1er cas : Transformer une rotation en une translation

2ème cas : Transformer une translation en une rotation

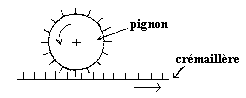
Le système pignon + crémaillère

La translation de la crémaillère entraîne la rotation du pignon et inversement. Le système est réversible. (ex : le cric de levage)

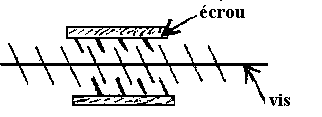
Le système vis + écrou

Selon les conditions, la rotation d'un élément entraîne un mouvement de translation et inversement lorsque le système est réversible. (ex : étau, cric, tournevis automatique, toupie)

Le système bielle + manivelle

La translation de E entraîne la rotation de S et inversement par l'intermédiaire de la bielle et de la manivelle.

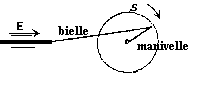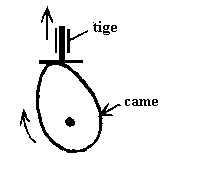
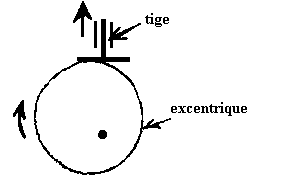
Les cames ou les excentriques + tige

La rotation de la came ou de l'excentrique entraîne la translation de la tige . Le système est non réversible.

Auteur : M. VERLAINE - TECHNOLOGIE I.U.F.M. ARRAS